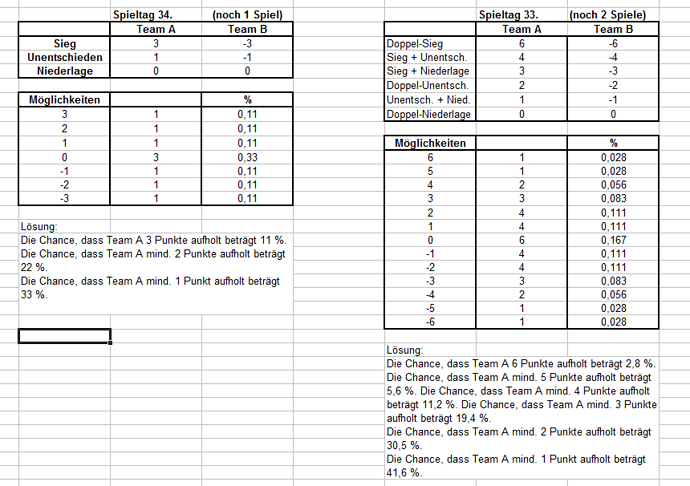
Aaalso, Trinome lösen wirklich einen sehr einfachen Fall, nämlich: Team A liegt unmittelbar hinter Team B, mit m Punkten Rückstand, alle folgenden n Spiele sind zwischen Team A und Team B.
Wenn Du das für realistische Spieltabellen und Spielpaarungen brauchst, dann sind die Wahrscheinlichkeiten pfadabhängig, sprich 5 Punkte in 3 Spielen aufholen geht allgemein nicht mehr durch einen Sieg und zwei unentschieden. Es muß noch sichergestellt werden, daß Team B in den nächsten drei Spielen verliert.
Der Lösungsansatz hier ist: Man simuliert alle erdenklichen, legalen Kombinationen (und nennt deren Anzahl X), dann selektiert man die, bei denen A mit B mindestens gleichgezogen ist (nennt deren Anzahl Y) und dann ist die Wahrscheinlichkeit Y / X (immer mit der Gleichverteilungsannahme).
Für Spiele bei denen A gegen B spielt, haben wir die Lösung mit den Trinomen bereits. Wenn A mal nicht gegen B spielt, dann betrachtet man die möglichen Spielausgänge (aus Sicht von A und aus Sicht von B), also SS, SU, SN, US, UU, UN, NS, NU, NN, also A siegt, B siegt, A siegt, B unentschieden, usw. Fürs Aufholen von Punkten heißt das 0 (SS), 2 (SU), 3 (SN), -2 (US), 0 (UU), 1 (UN), -3 (NS), -1 (NU), 0 (NN). Du ahnst es vielleicht schon, aber wir müssen noch multinomialer werden und wollen die Koeffizienten von:
(x^-3 + x^-2 + x^-1 + 3x^0 + x^1 + x^2 + x^3) ^ n
ausrechnen, also ein 7-nomialer Ausdruck statt eines trinomialen.
An dieser Stelle mußt Du Dich entscheiden, ob Du eine schöne geschlossene Formel haben willst, wo Du nur einsetzen mußt: m Punkte, n Spiele, davon r Spiele zwischen A und B. Oder ob Du nicht einfach vollständig simulierst.
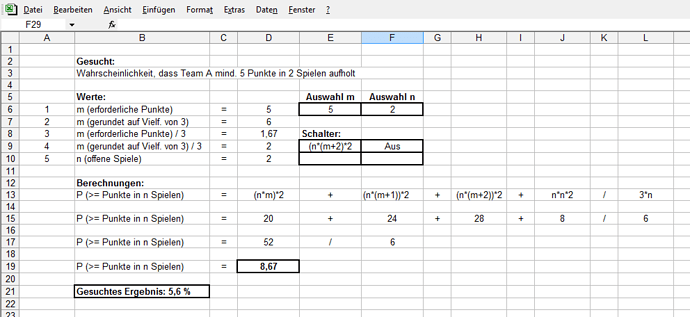
Ich sehe Du willst das ganze in Excel machen? Da scheidet die Simulationslösung ja schon fast wieder aus, und auch die Lösung per Multinomialkoeffizienten in Ermangelung an Mathefunktionen, die man dafür bräuchte. Ich bin aber auch kein Excel-Experte.
Dann zu dem Rest der Fragen: Ja, die Trinomialkoeffizienten (und später die 7-nomialkoeffizienten) müssen aufaddiert werden und durch 3^n geteilt werden. Ich hoffe, Du weißt das 3^n und 3*n was ganz anderes sind.
Die Schreibweise … sollte anschaulich die Schleife darstellen, in der Mathematik nimmt man dafür das Summenzeichen, was ich aber hier nicht tippen kann: Also Summe von k=(m bis n) über [n k]2. Später steht hier dann Summe von k=(m bis n) über [n k]6.
Für die Punkte hatte ich vorgeschlagen nur ein Drittel zu nehmen, weil man dann einfach die Formel von Wolfram abschreiben kann. Ansonsten kann man auch das Trinom (x^-3 + 1 + x^3) ^ n und entsprechend steht dann in der Summe [n k]2 * x^(3k) (es ist wirklich schade, daß man hier keine mathematische Notation tippen kann), und man muß nun „k passend starten lassen“ also bei 5 Punkten braucht man k=2 denn 3k = 6.
Zum Thema aufrunden, ja man muß auf das nächste durch 3 teilbare Vielfache aufrunden.
3^4 Tupel war konkret ein Beispiel für 4 Spieltage, allgemein sind es 3^n.
Ja Gleichung 11 definiert ja gerade was [n m]2 als Zahlenwert zu gegebenen n und m ist. Was hast Du denn stattdessen gerechnet?
j ist der Summationsindex bei Wolfram um [n k]2 auszurechnen.
Auf dem Taschenrechner mußt Du die Summe natürlich selbst ausrechnen. Aber für diese (n j) (n über j) bzw. (2n - 2j n - k - j) gibt es auf den Taschenrechnern (meistens) eine Taste nCr (n choose r).
Ja eckige Klammern sind bei mir nur Notation für die Trinomialkoeffizienten gewesen [n k]2 soll heißen „n über k zwei“, so wie bei Wolfram definiert. Wie gesagt, ich kann die Notation hier nicht herkopieren. Und die 2 steht für Trinome, in Anlehnung an Binomialkoeffizienten, wo da im Index eine gedachte 1 steht.
Die geschlossene Formel ist eine Gleichung mit Parametern, die muß nicht variiert werden.
Allgemeingültig wird dann die vollständige Betrachtung mit den Spielen, in denen A nicht gegen B spielt. Da solltest Du mir noch die Rückkopplung geben, ob Du das mit einer fertigen Formel machen möchtest. Es wird dann einen Parameter mehr geben, nämlich in wieviel Spielen der nächsten n Tage die Paarung A vs B auftritt.
Die Alternative per Simulation ist zwar bedeutend einfacher zu verstehen und zu programmieren, aber auch langsamer, und man braucht wie gesagt vielleicht etwas besseres als Excel.