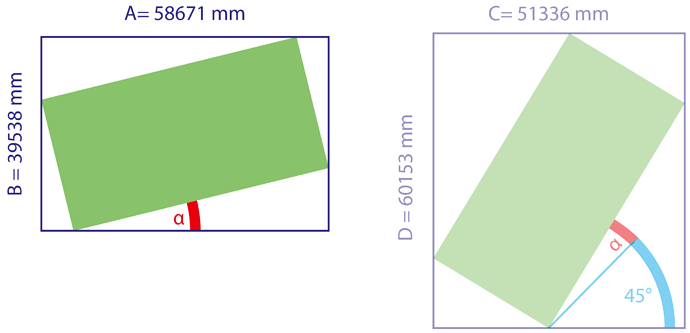
Diese Formulierung war missverständlich. Gemeint ist wohl, daß, wie in der linken Graphik, daß der zu α addierte Winkel 0° beträgt. So, wie in der rechten Graphik der zu α addierte Winkel 45° beträgt.
Das geht aber nur, wenn das grüne Rechteck eindeutig bestimmt ist. Du schreibst aber, daß dessen Seitenlängen unbekannt sind. Du hast für die rechte Graphik das Rechteck aus der linken also einfach kopiert?
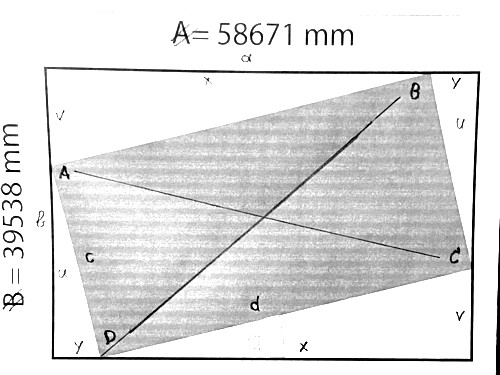
Hier mal eine die Graphik mit Kennzeichnungen:
Nur, wenn das Rechteck [cd] bzw. [ABCD] festgelegt ist, dann sind die Seitenlängen des Einbettungsrechtecks [ab], das durch das Anlegen eines Schenkels „x“ an „d“ mit dem Winkel α erzeugt wird, eindeutig bestimmt.
Denn umgekehrt, in einem gegebenen Rechteck [ab] (= in deiner Graphik [AB]) lassen sich (in einem wohldefinierten Geltungsbereich) unendlich viele Rechtecke einbetten, mit je einem eigenen Winkel α. Wenn bei dir also das eingebettete (=grüne) Rechteck beliebig ist, dann ist α nicht bestimmbar.
Folgende Überlegung: Werden zwei Punktepaare [A,C] und [B,D] In einem gegebenen Rechteck [ab] punktsymmetrisch angeordnet, dann bilden diese im allgemeinen ein Parallelogramm. Sie bilden ein Rechteck genau dann, wenn dessen Dialogalen gleich lang sind. Hier sind die Diagonalen [AC] und [BD].
Es gilt dann mit
a = x+y
b = u+v
[1] [AC]² = a² + (u-v)² = a² + (2u-b)²
[2] [DB]² = b² + (x-y)² = b² + (2x- a)²
→ [AC]² = [DB]²
→
[3] u(u-b) = x(x-a)
bzw,
x[a-x) = u(b-u)
Das ist (logischerweise) konsistent mit
[4] (b-u)/x = tan α = (a-x)/u
Für ein gegebenes x (d.h. für eine gegebene Seite c des eingeschriebenen (= grünen) Rechtecks ergibt sich die Gleichung für u
[5] u² - bu + x(a-x) = 0
[6] u = b/2 ± √(b²/4 - x(a-x))
Daraus und mit [4] ist dann auch α bestimmt.
Und daraus ergibt sich auch, mit x/c = cos α, daß bei gegebenem Einbettungsrechteck [a,b] alle (!) diejenigen eingeschriebenen Paralleogramme [ABCD] bzw. [cd] Rechtecke sind, für die gilt:
[7] b²/4 ≥ x(a-x))
für die also die Wurzel in [6] reell ist.
Also bei unbestimmtem grünen Rechteck, eingeschrieben in das bestimmte Rechteck [a,b], ist auch der Winkel α nicht bestimmt.
In deinem Beispiel könntest du x graphisch bestimmen, daraus mit [6] u berechnen und daraus mit [4] den Winkel berechnen. Ich komme auf etwas zwischen 13,5° und 14°. Wurde ja so auch auf anderen Wegen gefunden. Aber, wie gesagt, nur unter der Bedingung, daß daß das Seitenverhältnis des grünen Rechtecks als bestimmt gilt.
Gruß
Metapher
![]()
![]()